Hi
It's a very interesting and difficult quiz to solve inside moi. Looking at the math makes me dizzy. :)
I kinda solved it inside the nodeeditor by brute forcing the quiz conditions. (With 0.005% tolerance)
Take a look at attached file.

Hi MO,

My nodeeditor has the wrong node, infos>Display
Where is the latest Display node? I have Jame's Sept 14, 2020 nodeeditor version. Is it still the latest?

Also, I do not have the "Blue/Green/Teal" nodes which have one input, and have Title, Style, and Edges, where the Title serves as a label.
Where is a copy of this node located?

After replacing Display node, and removing the several "label" nodes, your script ran.
Your Radius shows as 0.9293, for Scale X = 1
The length of your 4 unit chords are different, and do not equal 1 unit.
zooming way in shows top and left points slightly outside of the circle.

-Thankyou
- Brian

Hi All,

I think I've solved it, though there are few very tiny errors...



So I made plenty-plenty trial n error by rotating the green circle (on the right) with A2 as its pivot. Every time I rotate this circle, I make a 3pt Circle (red) through A1,A2, and B, to check if this circle intersect all this circle, green circle, and vertical axis in exactly one point... The goal is to make this red circle touch all of A1, A2, B, and C where C must be on the Vertical Axis. It's very impractical but does the job, I guess..

As you can see, there is very tiny difference at the red circle radius where the vertical radius has a 0.0000001 deviation from the other. Also, the angle of C and B differs about 0.0000011 deg. I think this is good enough (?)

I'm still looking forward for much simpler and better solution, though... so please write anything should you feel necessary.

Cheers!

Here is another one. It respects the 2 statements "x" and "x * square root(2)".
The key is to circumscribe the pentagon instead of inscribe it.
With circumscribing, it is possible to use Tangent snapping.
Mirror History and rotation to tangency are essential to "fit" the sides.

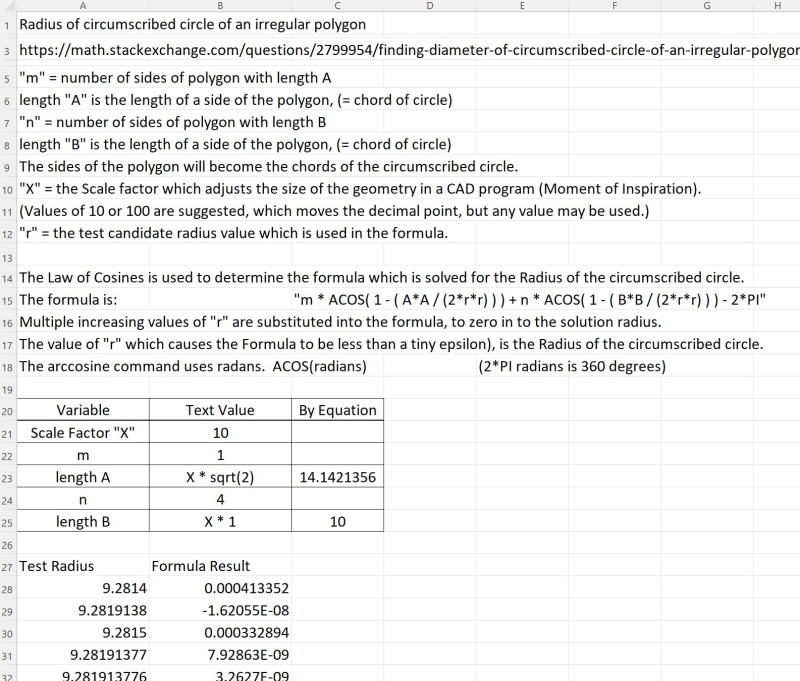
I dd an Excel spreadsheet to calculate the Radius, semi-manually.

A scale of X = 10 was used.
MoI seems to allow a setting of 7 decimal places.
Note: A scale of 1000 with 7 decimals does not seem to work well in MoI, as far as snaps and intersection went. (?)

At X=10, the best Radius, limited to 7 decimals, was 9.2819138 units
In Excel, the error was -1.61E-8

A more precise Radius, with 13 decimals, was 9.2819137798526, with error of 2.50733E-12, BUT I think that this value is unusable in MoI (?)

At X=100, the best Radius, limited to 7 decimals, was 92.8191378, with error of -1.16072E-10.

So there is not a "Perfect" solution, with the number of decimal that can be used. The radius value might be transcendental.

The Excel formula in cell B29, which references the variable values, for Radius cell A29, is:
=$B$22*ACOS(1 - $C$23*$C$23/(2*A29*A29))+$B$24*ACOS(1-$C$25*$C$25/(2*A29*A29))-(2*PI())

The Excel spreadsheet is attached, and with a little practice, anyone can build one. Spelling error, radans should be radians. (ACOS() uses radians not degrees of angle.
I learned the rudiments of Excel many years ago.

- Brian

So the puzzle can be built in MoI, using the "best" radius of 7 decimals, at X = 10, or X = 100.

Hi Brian
-- My nodeeditor has the wrong node, infos>Display

I'm not sure which version I'm using. Maybe mine is the one that is outdated.
The "Display" node initially was inside "r2d3" menu.

-- Also, I do not have the "Blue/Green/Teal" nodes

These nodes are "output" nodes that I changed their colors and used as label. (right click on the node >> "colors")
Also, you can double click on the canvas. This way the node's name and address will be displayed in the properties panel.

Hi, Mip...

But part of the quiz is all of the vertices MUST be in a circle circumference...



So, from the screenshot, if you pick any 3 of the 5 vertices as references for a 3 point circle in Moi, then ALL of them should be exactly on this circle circumference.

Hi, Brian...

That looks very sophisticated for me. ^_^;
I really wish that I'm as smart as you in math.

Thanks for the help and effort.

Cheers!

Thank you MO.

- Brian

Hi Elang

Congratulations on solving the puzzle!
Your numbers and angles look about as good as they can be, given 7 decimals of precision, at X = 10.


After carefully redrawing as X = 10, with radius of 9.2819138, these are some values realized:
Radius = 9.2819138 (This value might be slightly too great, in decimal 7.
Angle A = 97.781889
Angle B = 114.812072
Angle C = 114.812074 (Slightly different)

These numbers are nearly the same as your numbers, +/-.

Construction can use a variety of MoI commands.
Zooming in a huge amount, shows very slight anomalies

I do not know if X = 100 would make much difference. Maybe pick up an extra decimal.

- Brian

Hi Brian

Thank you for kind words. I've got lots reference from all posts here which led me to solving the problem which I appreciate very much. Now if only the process I've been through can be automated, it would be very nice. Perhaps via some script?

And yes, zooming in huge amount will show anomalies, but I guess this is natural since the precision is not infinite in every ways possible.

Cheers!

Hello Elang,

I wonder how I missed your post! As I love geometric puzzles!

I think by now you have solved your puzzle, However I would like to examine a possible solution myself, so, please answer the following questions:

> So we provided with 3 lines:
> - 1 horizontal blue line with length of X√2
> - 2 magenta lines with length of X

> The task is to arrange them in specific ways so that: they form a continuous polylines with each endpoints are exactly on a perfect circle circumverence (red circle), like in the provided illustration (it's actually not an acurate drawing I
> made in Moi). The real task is to form a pentagon with 4 magenta lines (length = x) and 1 blue lines (length = x√2), but I believe we can ignore the other 2 since they'll be added later by mirroring the 2 existing magenta lines horizontaly.

1- the pentagon should be regular or it could be irregular? (I know if the blue line is going to be the base of the pentagon then we are talking about irregular pentagon I also know u have mentioned it! however, I need to be sure.)
2- Tell me if we are provided by all the mentioned lines. (or should we make a line from other line? for example blue from red?)
3- Tell me about the initial position of the 3 lines!

- Psygorn

I think that the desire was that TWO of Four X length lines (chords-to-be), are to be placed or moved, perhaps by Rotation, until some snap is achieved, (perhaps at apex).

The trouble is that as the base angle changes, the other 3 angles change, and there seems to be no way to achieve a Snap solution.
(The other 3 angles are equal to each other.)

The angle at B is a function of the base angle at A2, so as the (chord) rotation occurs at A2, if there was some way to Constrain the angle at B, by said formula, a snap to the top center of an increasing 3pt circle might be possible. (???). History of 3 point circle does not seem to occur for movement of the 3rd point in its creation AFAIK.

Constraint of 3 angles to be equal, based upon change in degrees of a 4th (base) angle does not seem to be available in MoI(?)

- Brian

Another factor is that the value of the solution radius turns out to (seems to) have more than 12 decimal digits, so perfection may not be possible, given floating point limitations.
So a solution within a small epsilon is acceptable, IMHO.

The 4 chords can be on the circle, but have slightly different lengths,
or the chords can be of equal length, but two of the vertices be slightly outside of, or inside of, the circle...IMHO
And/or slightly different angles...

Not yet all read above but here my solution as usual very rustic brute force by "hand" but...i obtain the solution! :)
Circle by 3 points and big zoom for draw some tests :) Maybe 20! :)
AB = hypothenuse of a rectangle triangle 1*1 * hypo

I found the solution with 0.1234567 decimals permitted by Moi!

Radius found of the red Circle : 0,9281914 (max definition)
Here x = 1
Five points of the pentagon will be on the circle!

Of course when you have this first solution any resize will give you the other infinite solutions! :)

After the third C point i ask the length of the segment... if not 1 i draw another one C ! (up or down following results) :)





https://moiscript.weebly.com/uploads/3/9/3/8/3938813/longueur1.3dm

Ps seems there is something ultra simple that i have seen in writing this! :)

Intolerable suspense! :) I must verified my intuition!

Hi MO (MO_TE),

When I load "pentagon_Quiz.nod" the nodeditor's run button looks deactive (meaning it does nothing)! What could be the reason? How can I fix it?

- Psygorn

Hi, Psygorn... sorry for late reply.

1. Yes... it would be an irregular pentagon with: 1 edge length = X√2 while the other 4 edges length = X
2. The necessary elements is all mentioned already.
3. Actually, there is no specific initial position for the lines except it would form an irregular pentagon like mentioned in point 1, AND if we draw a 3 point circle through 3 vertices of the pentagon then ALL vertices should by on the circle circumference.

Cheers!

Hi Pilou,

That's very much similar of how I solved the problem.

:)

yes very "physcical" it's the less headaches! :)
Only result is counting!
I will continue to find something very simple! ...

Hi psygorn
Sorry about that.
I guess it has to do with the "display" nodes I used. ("NE" old version).
Wrong nodes have a red box on their upper left corner.
You can delete them or replace them with similar nodes.

Also I tried to make a more accurate pentagon. " pentagon_Quiz_Loop_Method.nod "
This time I used "loop" nodes. Give it a few seconds to see the pentagon !

So close! :)

Hi Elang,

I know as of now you have already solved the problem.

However, I think I might be able to correct your calculations a bit further.



Though I think it is a difficult problem for your nephew. But if he has more of these puzzles I would be happy to see them :-)

Remember alpha can have different values I chose the value that helps solving the problem.

The numerical method was done using a pocket calculator. So, maybe there are methods to calculate it with even more accuracy.

Do not take the last digit as granted. and for two alphas I think you can assume it is equal to 114.8120745 degrees.

If u use this amount then Angles A,B & E would all be equal to 114.8120745. However, even in this situation when u superzoom into it there u can see the corners are not on the big circle (which I think is not a calculating issue, it is rather displaying issue which I personally believe u can safely ignore it.)

And I failed to find a simple genius method to solve this problem, maybe there isn't such a solution. However, I cannot be sure!

- Psygorn