Full Version: UnwrapCurve plug-in

Show messages:  1-11  12-31  32-51  52-71  72

Hi Burr,

> "I used scale from center", to bring the point stucture into length with
> the new line... Does that distribute them "Properly"? or is it just close.
> Would a "stretch" be different? Like distorting it more?

The problem is that it's not only the control point spacing that controls the parameterization of a curve (or of a U or V direction in a surface) - part of the information that makes up a curve is also a knot vector which also controls how the parameter space of a curve is formed.

That kind of control point spacing that you show there would be correct if the original curve had a uniform knot vector, but not if it had a non-uniform knot vector, if it had a non-uniform knot vector that knot vector would also need to be used in your new curve as well.

When you draw a new control point curve, it gets a uniform knot vector, one with even spacing between the knots.

You could solve what you show there by reconstructing the surface to have arc-length parameterization, that will then make it have a distance-based parameterization and so it will behave the same as a line, then you do not need to try to recreate any control point spacing.

You would reconstruct that extruded surface to have arc length parametrization in its bendy direction by extracting out the profile curve, running Rebuild on it with the refit to tolerance mode, and then re-extruding the rebuilt curve back out again.


But often if you're just using an extruded surface in surface-to-surface flow you can just get the same result by using curve-to-curve flow instead and like I mentioned previously curve-to-curve flow is itself based off of distance traveled along each curve and so it not sensitive to parameterization at all.

Do you have some flow example that you could show where you think you need to recreate that control point spacing? I can then show you how to avoid the need for it - the answer will be though to either use Rebuild on your curve before constructing a surface out of it or to use curve-to-curve flow instead of surface-to-surface flow.


- Michael

---

Hi Burr, and now that I see that you just squished the control points down by scaling - no that's not how you would maintain the proper spacing in any case, you would need to measure the distance along the entire control polygon and then measure the percentage distance of each particular point along that polyline, and that percentage is where you would place it on the line. But like I mentioned before that would only work if the knot vector on the original curve is a uniform knot vector.

It should not be necessary to do any of that at all though, either doing Rebuild or doing curve-to-curve flow would avoid any issues with uneven parametrization.

- Michael

---

GHi Michael,
great explanation... I posted that before I saw your first response to Majik about that... My post was aimed at Majiks solution of building a revolve surface with the same point structure as the target, to use as a base for flow, But I think you answered that now... And also my question that just scaling doesnt produce the same "percentage spacing" as would need to be calculated for a proper points spacing.

Thanks for the time.

---

Thanks for the explanation Michael,

Before, when doing the revolve methods, I've had to create a spline "by eye" to get point spacing that was somewhat representative.

A case where I can think of where the need for this kind of spacing directed towards flow would be the design of art detail on the rounded surface of a ring.
Where you would want the art spaced on surfaces with concaved and curved elements. Or in a case where there are undulations in a surface that needs concise art to be flowed on it.

...but, there's generally an alternate solution to everything. ;-)

However, there have been many cases just in my adventures in the t-shirt and sign industry where having representative lines with exact and straightened information from curved sources is useful.

---

Here is an example that works for me, you can select an edge curve or 2 and run the script
This generates the two lines behind , that are the length of the edges laid out flat
You can then easily make the planar surface that is the correct length and width to match the target surface and use flow to wrap the text or other objects to the surface.
Brilliant



I made an even better example

Image Attachments:
ScreenShot855.jpg  ScreenShot856.jpg 

---

Hi Mike,

> Before, when doing the revolve methods, I've had to create a spline
> "by eye" to get point spacing that was somewhat representative.

Do you mean that you were altering the spacing to intentionally introduce uneven spacing and compression in some areas and squishing in other areas?

Or do you mean you were trying to eliminate that and have an even mapping from the base plane to the revolved surface?

Because if it's the latter and you wanted an even mapping, you could have achieved that by just drawing the revolve's profile curve any way that you like to start with, and then before revolving it do a Rebuild on it (with Refit to tolerance mode) - the result of the rebuild will be free of squishing or stretching in its parametrization and that will inherit to the revolved surface as well.


> However, there have been many cases just in my adventures in the t-shirt
> and sign industry where having representative lines with exact and
> straightened information from curved sources is useful.

Yup, and this plugin will do that.

I don't quite follow where the replication of the control point spacing onto the line would be helpful though. If you have a specific example file where that would be helpful could you please post it so that I could take a look at it?

- Michael

---

Hi Shayno, yup that's a great use of it to get the proper proportions of the flat plane of the same length as the circumference of your ring!

- Michael

---

I may try to create a better example later to show what I'm seeing in my head.

Here is an example of what I do to mimic the "straightened out" spacing of a more complex curve in order to flow something to it.
In the following pic, there are two curves. The top one is a curve with all kinds of bends and curvy stuff happening to it. - representative of my target flow surface.
The lower curve is one I made by hand with a spline tool. - straight, to use as the reference surface. I had to guess to approximate how far it was between each control point, as if I was able to stretch the top curve out straight.
The c-lines are just there to show the relationship between the original curve and it's control points to that of the straightened-out version.



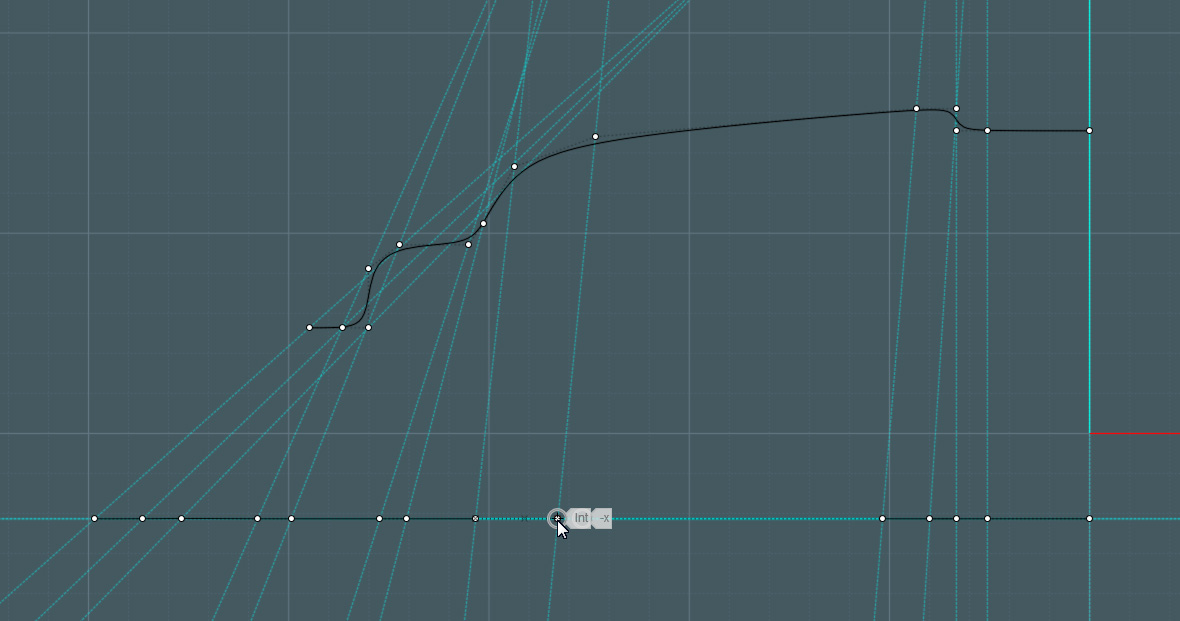
I used these curves to revolve them into circular surfaces, but it also works for a non-revolved flat surface if I simply extrude both of the lines to form rectangular surfaces.


Of course, just throwing control points along a straight line is not going to work accurately by eye, because the above control points of the shaped curves do not represent the true on-curve distance, they are used for spline control. But I can't think of any way to figure it out.

(man, is this an esoteric conundrum!)

---

Hi Mike, ok but what I have been trying to describe is that all you need to do is run Rebuild on that bendy curve and then after you have done that the rebuilt version of it has "arc length parameterization" - meaning that it will be a match to a simple single line as far as traveling along each in a uniform manner.

So if you want your revolve or extrude to have a "uniform traveling speed" matching property to a straight line, it's not necessary to construct such a complex multi-point straight line version of your curve like you are doing there, instead do a rebuild of your bendy curve before you construct your surface out of it and just have a simple regular line segment for the line.

Also note that none of this applies to curve-to-curve flow at all, it only deals with distance as traveled along the curve and so parameterization and control point spacing does not have any effect there.

Anyway, the key thing that I'm trying to explain is that yes - your bendy curve there that was drawn from Draw curve > Freeform > Control points has uneven parameterization as you currently show it. But if that uneven parameterization is going to cause a problem for you later on with surface-to-surface Flow then just run Rebuild on it (with "Refit to tolerance mode, not # of points mode), and the resulting rebuilt curve does not have uneven parameterization on it anymore. An even arc length parameterization is one of the properties of rebuild.

- Michael

---

> Hi Mike, ok but what I have been trying to describe is that all you need to do is run Rebuild on that bendy curve and then after you have done that the rebuilt version of it has "arc length parameterization" - meaning that it will be a match to a simple single line as far as traveling along each in a uniform manner.

Thanks Michael, that has awesome potential!

Let's take a look at how to implement this:

PREPARATION FOR FLOW BY USING REBUILD+UNWRAPCURVE



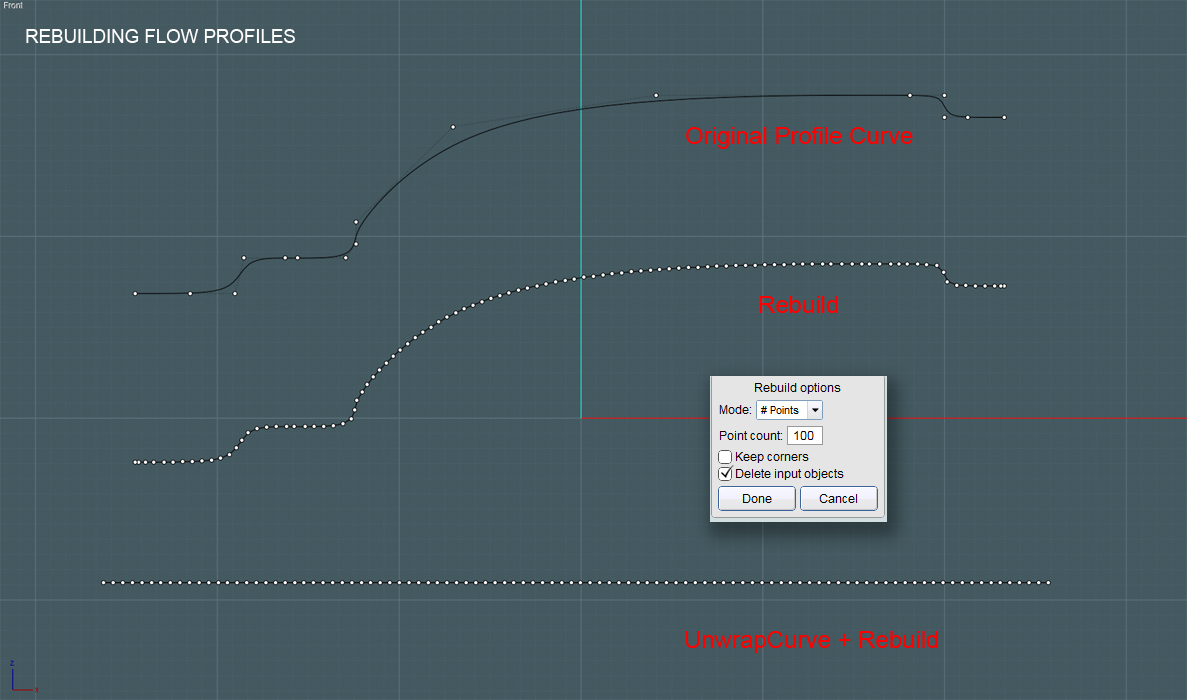
(looking at the pic)
The first curve at the top is the original spline representing the profile of our TARGET Flow surface.
The second curve in the middle was derived from the same profile curve using the Rebuild command. I chose 100# points, which as Michael pointed is used to build arcs or (near) even displacement along the curve's path.
The third line was derived from the profile curve using the new UnwrapCurve script.
It has also been rebuild (Rebuild) using 100# points, though it is still straight.

The advantage of using UnwrapCurve is to derive a line that is a close approximation of the true length of the profile curve when it is stretched out.
Therefore, when used as a Flow target, there shouldn't be too much overall length or dimensional distortion in the final result.
The goal is to make the original objects appear to flow along a surface naturally.

Now I'll use the profiles:
Note - You can also rebuild and unwrap curves (up to all four sides) to make a more complex Network.
In this case, I Extrude the profiles and the line in order to create Target and Reference surface to try Flow with.



As you can see in this pic, the underlying points (isocurve) structures of these surfaces are constructed from the points within the profile curves.
These underlying arrangements will determine the the final placement of the flowed objects regardless of the appearance of the surfaces.


Here, I'll create a nice pattern to be flowed onto a surface created from my original profile:



I chose these pentagon/circle shapes to make a test pattern. Their shapes make it easy to see any relative distortion on the spatial arrangements when flowed.


And here is the result!:



The Flow result on the top surface derived from the original profile curve has an awful displacement. (awful for what I needed in this instance) The distortions follow the "parameterization" of the control point arrangement in the original spline. This effect has advantages too and allows you to do neat things where this type of distortion is needed.

Ah! And you can see the Flow result in the middle. It has a very consistent-looking displacement.
For the Flow placement of shallow object arrangements, you can get very natural results this way.
Of course, the displacement of a flow is most accurate at the base surface level. As you move through the W (above and below) of the surface, distortion will occur due to the variances in the angular re-arrangements of the flowed objects. In other words, pinching and expanding will naturally occur.

I'm curious to try both a U and V arrangement.

---

Cool. I sense a new round of creativity is about to begin :)

Ed

---

yeah,... lol...

Peace,
Rich_Art. ;-)

---

Oh the shear power and glory!
Michael throwing new scripts and features into the mix is like throwing fresh meat into a shark pool. ;-)




Oh yes... there is much potential here.
Though there is a little distortion along the middle, these Flowed objects placed quite well.

With this model I first made a ring shape by Sweeping a single arc around two bent circles.
I didn't use the surface created by the sweep, but I was able to project some lines to give me some accurate arcs.

All four boundary arcs were Rebuilt to 50# points. I made an extra one in the middle to help with making the Network.
So I made a 50x50 isocurve surface with Network for the side of this ring shape.

I used UnwrapCurve to make the four lengths needed for the planar reference surface.
I had to approximate the arc curve for the sides. Flattening one of the original arcs in an "ortho" direction helped make that.

I made sure to Rebuild the flat curves to the same number so that the two surface would jibe when Flowed.

A method like this means I have more control when Flowing art, type or patterns on something like a ring.
I didn't have to contend with squeezing or anything strange... I know some of you are itching to try this out!
Not that this could not be more easily achieved by guessing and going for a straight flow, but this works so well. ;-)

---

Hi Mike, those are great looking results!

You may want to use the "Refit to tolerance" mode for the rebuild though (try with a tolerance of 0.001), since that mode is able to add more detail to the rebuilt curve only in areas where it is more bendy, while at the same time giving a result that has an evenly distributed parametrization.

Also you should get the same results that you show with just leaving the line totally alone, you should not need to rebuild the line.

There is not any need to actually get the exact same number of control points in both the base and target curves - what you instead need is for each curve to have an evenly distributed parameterization which a line will already have without rebuilding it.

- Michael

---

Thanks for the pointers!

> You may want to use the "Refit to tolerance" mode for the rebuild though (try with a tolerance of 0.001)



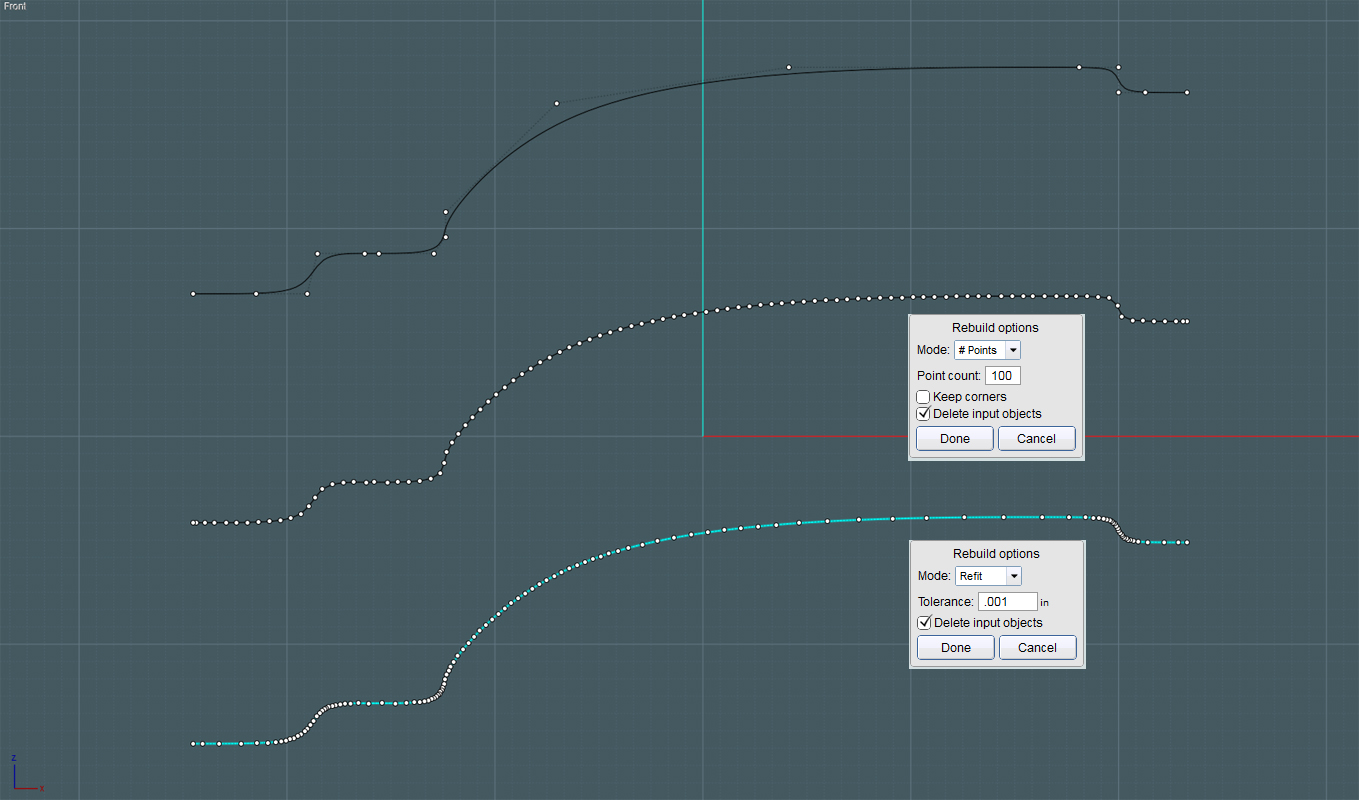
Ehh... :-/ For some reason, that way ends up with unevenly distributed points.

---

Hi Mike,

> Ehh... :-/ For some reason, that way ends up with unevenly distributed points.

Yes it does, and it's supposed to - it adds more refinement in areas that are bendy.

But it also at the same time uses a knot vector spacing for the generated curve so that the parameterization matches that point spacing.

So the actual curve that is generated there has an even parameterization and will generate the same kind of "no stretching or squishing" result even though it has a non-uniform distribution of control points.

The key quality of the curve that you want to have is not actually "evenly distributed control points" - the thing you are looking for is actually "evenly distributed parameterization". The result of Rebuild with "refit to tolerance" mode will deliver that despite having non-uniform control point distribution.

- Michael

---

"evenly distributed parameterization".

Something we dont/cant see.... Part of the underlying definition of the geometry.....

---

Like how sausage is made.... ;-)

---

Oh, thats just wrong.... (or is it right?)

---

Hi Burr,

> Something we dont/cant see.... Part of the underlying definition of the geometry.....

Yup, the parametrization comes from one of the pieces of data that makes up a NURBS curve - the "knot vector".

The data for the knot vector is just a list of increasing numbers like this for instance: 5, 6, 10, 20, 52

That knot vector there for example makes a curve that has a domain of 5 to 52 - that means that for every value between 5 and 52 the curve can be evaluated at that parameter value to produce a point location. That numeric range from 5 to 52 is the "parameter space" of the curve - a one-dimensional space that's part of the curve definition. Surfaces have 2 knot vectors, one for the U direction and one for the V direction and so they have a two dimensional parameter space.

The knot vector is not something you usually see directly because it would involve some huge spew of super techno-geek information that you would not particularly be able to do anything with.

But the knot vector comes into play in the overall mechanics of how the NURBS curve works - the relative spacing between different knots is one thing that affects how much influence the control points in that region of the curve have on the shape of the curve. Just to complicate matters there is also another totally separate type of data called "weights" that can also affect a control point's influence but the weights exist primarily because the particular type of influence they have is able to be leveraged to produce exact conic sections.

Being able to have different spacing between knot values is what gives the "NU" to NURBS, the NU stands for "Non-Uniform".

One of the main reasons why it is good to have this ability to do different knot spacings is to be able to more naturally set up interpolation through data points that deals better with the data points having some different spacing between them. When you try to interpolate an uneven distribution of points with a uniform spline (uniform means a knot vector with all equal spacing between all the knot values), it basically tries to produce the same length curve spans between each point and that makes for a sort of excess amount of curve being left over in areas where the points come closer together and that excess curve area makes for curly-cue type shapes in those areas.

The Rebuild command with the "fit to tolerance" method produces a curve that has a non-uniform knot spacing, but the spacing is based on the distances between the interpolated data points, so it matches the point spacing and makes the parameter space relate evenly to 3D space.

I've tried to make MoI set up in general so that you don't have to worry so much about these kinds of things, but it so happens that parametrization does come into play with surface-to-surface flow. I was able to make it not an issue in curve-to-curve flow since it is possible there to map distance traveled along each curve rather than just mapping parameter values from the base curve to the target curve. With a surface it's not so easy to do that since a surface can be warped and bulgy in multiple directions and have different distances across it in different areas.

And then to make things even more confusing, I guess it's even misleading when I wrote "evenly distributed parameterization" - to be more correct I guess it's more like "consistent distribution of parameter space as to 3D space".

- Michael

---

Show messages:  1-11  12-31  32-51  52-71  72