Show messages: All
1-9
10-16
From: Zooen
Thank you bemfarmer for this Archimedean-Spiral wind turbine.
It's very promising for clean and ecological energy production; a wind turbine that respects the environment and is much less expensive than the traditional wind turbine.
Let's wish it a happy future, if the lobbies...
And what's more, there's a little 3D model you can make with MoI, which is very nice and educational.
From: Zooen
I didn't know that Archimedean-Spiral wind turbines could also be made of sheet metal and mounted on a wall,
or that they could be mounted on a kind of motorcycle with rather unusual tires!
From: bemfarmer
Thank you Zooen.
I will soon be making a conical log version, (which is less efficient than the Archimedean version, per post 13), as time allows.
- Brian
From: bemfarmer
After much confusion, I finally found a paper which clarifies the spiral used in the ASWT.
Spiral Wind Machine turban blades, (SWT or ASWT), are based upon either the golden logarithmic spiral (~ Fibonacci spiral) (log SWT), or the Archimedean spiral (ASWT).
Reference:
https://www.cell.com/heliyon/pdf/S2405-8440(23)04244-5.pdf
Quote from this reference:
"... The main findings from the presented examination proposed that the seashell-shaped wind turbine with the Archimedean spiral profile achieves better performance than the logarithmic profile..."
"7. Also, the Archimedean spiral seashell turbine of θ = 60◦ has the best operating range of all other configurations of the turbine."
The OLD conventional Archimedes wind turbine had multiple turns (AFAIK), and as per item 8 of the paper: " Additionally, the seashell-shaped wind turbine of the Archimedean spiral profile has a better performance than the conventional Archimedean turbine studied previously."
*****
the Fibonacci spiral.:
file:///C:/Users/orcha/Downloads/192-406-1-PB%20(1).pdf
As Fibonacci spiral:
https://www.researchgate.net/publication/351006076_DESIGN_FABRICATION_AND_ANALYSIS_OF_FIBONACCI_SPIRAL_HORIZONTAL_AXIS_WIND_TURBINE
- Brian
From: bemfarmer
Archimedes screw flight calculator, for developed (flat) annulus ring.
The UTube video with the formulas, and two errors (dprime and Dprime):
https://www.youtube.com/watch?v=PsBhPurfiG0
The Archimedes screw can be an conveyer auger, and has an outer and inner helix.
One turn may be constructed from an annulus, (ring or washer).
The annulus for one turn, (a 'Flight") will exclude a small wedge.
Pitch is the distance between two adjacent threads of the screw.
D is the outer diameter of the screw.
d is the inner diameter of the screw, and the diameter of the shaft.
Length is the Length of the outer helical curve.
length is the length of the inner helical curve.
Dprime is the outer diameter of the annulus.
dprime is the inner diameter of the annulus.
When several flat annuli are bonded together by their radii, and stretched along the shaft, like a spring, the outer and inner diameters of each annulus shrink down, until the shaft diameter is reached.
DprimeAngle, is the number of degrees around the annulus, excluding the absent wedge, and is equal to dprimeAngle.
dprimeAngle, is the same number of degrees around the annulus, excluding the absent wedge.
360 degrees minus DprimeAngle, equals the angle of the wedge.
360 degrees minus dprimeAngle, also equals the angle of the wedge.
length = sqrt(( d * PI ) ^ 2 + Pitch ^ 2 ).
Length = sqrt(( D * PI ) ^ 2 + Pitch ^ 2 ).
dprime = ( D - d ) / ((Length/length) - one ).
Dprime = ( D - d ) + dprime.
dprimeAngle = length / (( dprime * PI )/ 360degrees).
DprimeAngle = Length / (( Dprime * PI )/ 360degrees).
To unwrap the Archimedian Spiral Wind Machine blade, use Flow with source surface the one turn Archimedian screw that matches the Spiral parameters, and
target surface the Annulus. <<< To be tested>>>
- Brian
From: bemfarmer
After much study, the ASWT was re-modeled.
The blade Surface, formed in Moi, is "developable", and so can be Unrolled, (in Rhino 8), to a flat pattern with little or no distortion.
The blade Surface 3dm file was opened in Rhino 8, and the Unroll command was used to create a flat pattern.
The Flattened area was 2.3% greater than the blade surface area. Increase in "u" isocurve density in Rhino 8 made no visible difference.
No way to increase the "v" isocurve density was found.
The Rhino 9 Unroll command is very slow, perhaps 5 to 10 minutes. First it calculates the before and after Area, to give an idea of "distortion".
It was difficult for this novice Rhino 8 user to find the desired commands and settings, but some progress was finally achieved.
The blade is formed using an Archimedean spiral as a tapered Helix rail. The Helix is formed with the MoI Helix command, and tapers from maxRadius to zero.
The core cylinder region, "~shaft", is deleted from the blade.
The blade Surface is NOT an Archimedean tapered screw, nor a portion of a Toroid, due to the "open radius of theta = 60 degrees region", and how the two rails are swept.
(The rail spiral is NOT "logarithmic", nor "fibonacci".)
I may do a script or node, including updated "optimum" parameters, values and definitions.
And also check out how the actual degrees of the 3 blades, measured at a plane intersection, compare to the 60 degree, 45 degree, 30 degree (better) style.
- Brian
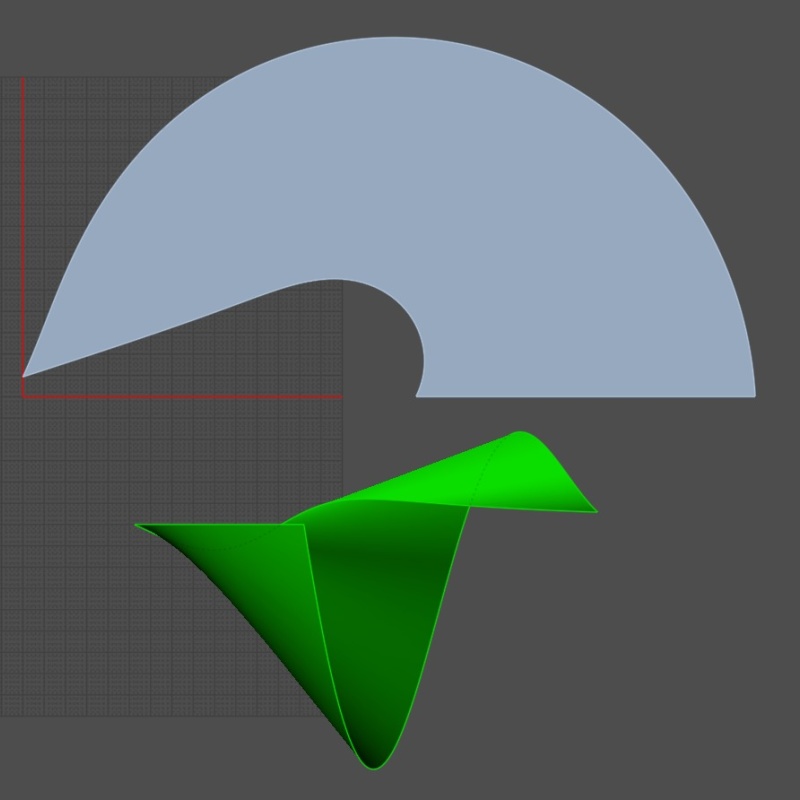
From: bemfarmer
There are said to be 5 types of helicoids.
The pictures in the links are hard to tell apart.
Scripting their parametric equations may help to discern the differences.
There are also many links to other, older, papers.
The ASWT may be a conical version of the Oblique helicoid, or of the Developable helicoid. (???)
V. J. Paul, “A review of geometry investigations of helicoids,”
https://www.researchgate.net/publication/325860850_A_Review_of_Geometry_Investigations_of_Helicoids/fulltext/5b29e65faca27209f374d62b/A-Review-of-Geometry-Investigations-of-Helicoids.pdf
Five Types of Ruled Helical Surfaces for Helical Conveyers, Support Anchors and Screws
https://www.matec-conferences.org/articles/matecconf/abs/2017/09/matecconf_icmme2017_06002/matecconf_icmme2017_06002.html
- Brian
Found some nice links to knitting as well.
Show messages: All
1-9
10-16
